Got a problem you’re trying to solve? Strategies like trial and error, gut instincts, and “working backward” can help. We look at some examples and how to use them.
We all face problems daily. Some are simple, like deciding what to eat for dinner. Others are more complex, like resolving a conflict with a loved one or figuring out how to overcome barriers to your goals.
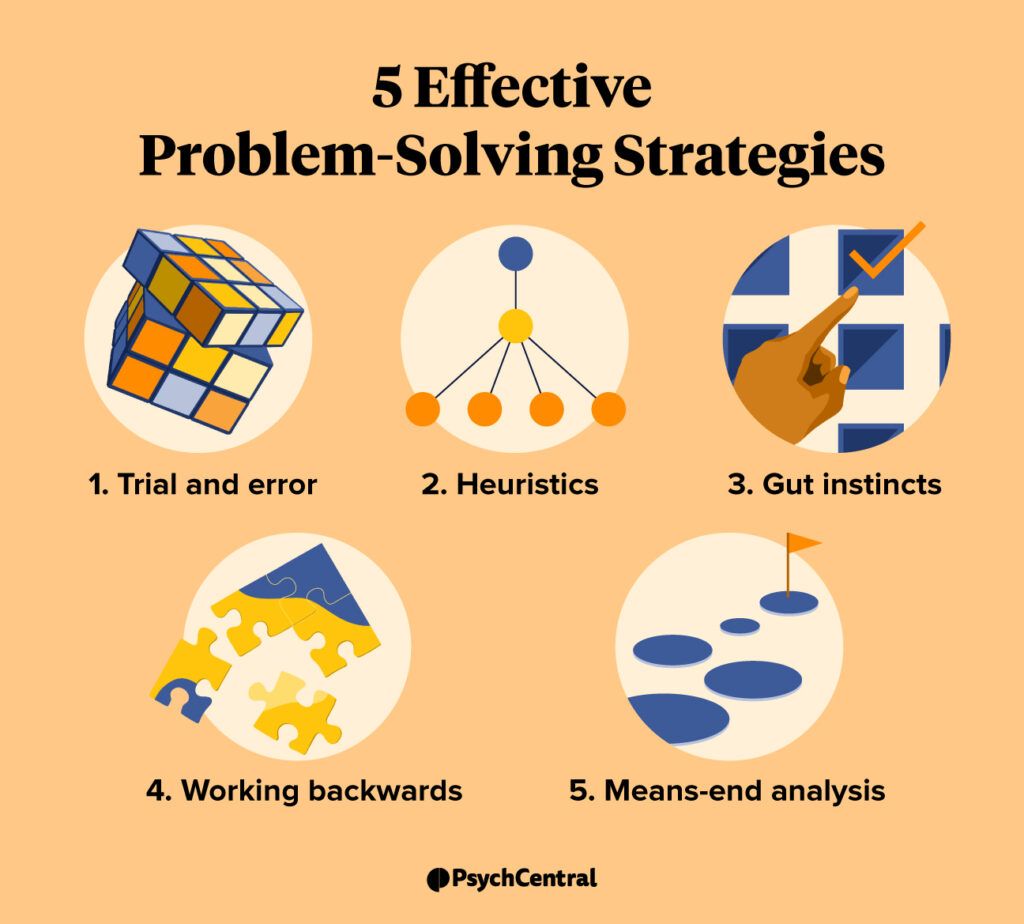
No matter what problem you’re facing, these five problem-solving strategies can help you develop an effective solution.
To effectively solve a problem, you need a problem-solving strategy.
If you’ve had to make a hard decision before then you know that simply ruminating on the problem isn’t likely to get you anywhere. You need an effective strategy — or a plan of action — to find a solution.
In general, effective problem-solving strategies include the following steps:
- Define the problem.
- Come up with alternative solutions.
- Decide on a solution.
- Implement the solution.
Problem-solving strategies don’t guarantee a solution, but they do help guide you through the process of finding a resolution.
Using problem-solving strategies also has other benefits. For example, having a strategy you can turn to can help you overcome anxiety and distress when you’re first faced with a problem or difficult decision.
The key is to find a problem-solving strategy that works for your specific situation, as well as your personality. One strategy may work well for one type of problem but not another. In addition, some people may prefer certain strategies over others; for example, creative people may prefer to depend on their insights than use algorithms.
It’s important to be equipped with several problem-solving strategies so you use the one that’s most effective for your current situation.
One of the most common problem-solving strategies is trial and error. In other words, you try different solutions until you find one that works.
For example, say the problem is that your Wi-Fi isn’t working. You might try different things until it starts working again, like restarting your modem or your devices until you find or resolve the problem. When one solution isn’t successful, you try another until you find what works.
Trial and error can also work for interpersonal problems. For example, if your child always stays up past their bedtime, you might try different solutions — a visual clock to remind them of the time, a reward system, or gentle punishments — to find a solution that works.
Sometimes, it’s more effective to solve a problem based on a formula than to try different solutions blindly.
Heuristics are problem-solving strategies or frameworks people use to quickly find an approximate solution. It may not be the optimal solution, but it’s faster than finding the perfect resolution, and it’s “good enough.”
Algorithms or equations are examples of heuristics.
An algorithm is a step-by-step problem-solving strategy based on a formula guaranteed to give you positive results. For example, you might use an algorithm to determine how much food is needed to feed people at a large party.
However, many life problems have no formulaic solution; for example, you may not be able to come up with an algorithm to solve the problem of making amends with your spouse after a fight.
While algorithm-based problem-solving is formulaic, insight problem-solving is the opposite.
When we use insight as a problem-solving strategy we depend on our “gut instincts” or what we know and feel about a situation to come up with a solution. People might describe insight-based solutions to problems as an “aha moment.”
For example, you might face the problem of whether or not to stay in a relationship. The solution to this problem may come as a sudden insight that you need to leave. In insight problem-solving, the cognitive processes that help you solve a problem happen outside your conscious awareness.
Working backward is a problem-solving approach often taught to help students solve problems in mathematics. However, it’s useful for real-world problems as well.
Working backward is when you start with the solution and “work backward” to figure out how you got to the solution. For example, if you know you need to be at a party by 8 p.m., you might work backward to problem-solve when you must leave the house, when you need to start getting ready, and so on.
Means-end analysis is a problem-solving strategy that, to put it simply, helps you get from “point A” to “point B” by examining and coming up with solutions to obstacles.
When using means-end analysis you define the current state or situation (where you are now) and the intended goal. Then, you come up with solutions to get from where you are now to where you need to be.
For example, a student might be faced with the problem of how to successfully get through finals season. They haven’t started studying, but their end goal is to pass all of their finals. Using means-end analysis, the student can examine the obstacles that stand between their current state and their end goal (passing their finals).
They could see, for example, that one obstacle is that they get distracted from studying by their friends. They could devise a solution to this obstacle by putting their phone on “do not disturb” mode while studying.
Whether they’re simple or complex, we’re faced with problems every day. To successfully solve these problems we need an effective strategy. There are many different problem-solving strategies to choose from.
Although problem-solving strategies don’t guarantee a solution, they can help you feel less anxious about problems and make it more likely that you come up with an answer.
